Cyberlympics CTF Kenya (1st Edition) - Write-up

Introduction

On Fri, 30th May 2025 — Sat, 31st May 2025, I lead Fr334aks-mini in an exciting Cyberlympics CTF competition an anchor program of the Africa Cyber Defense Forum (ACDF).

The Cyberlympics Kenya CTF (1st Edition) brought together Kenyan cybersecurity teams for a 24-hour battle across challenges like:

• Offensive Cyber Warfare
• Digital Forensics
• Cyber Defense
• Cryptography
• Web Application Exploitation
• System Exploitation
• Malware Analysis
• Reverse Engineering
• Cryptography
• Programming

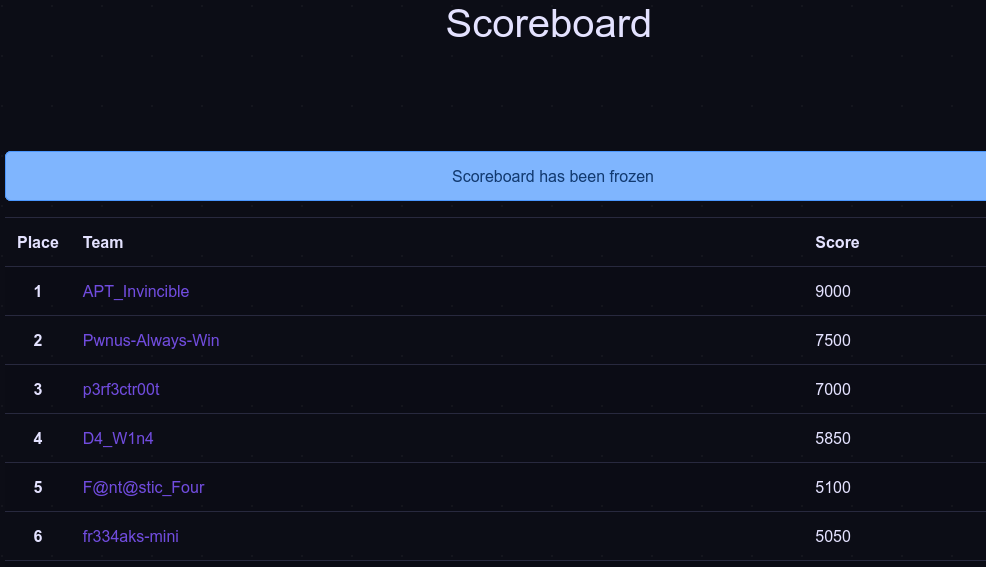
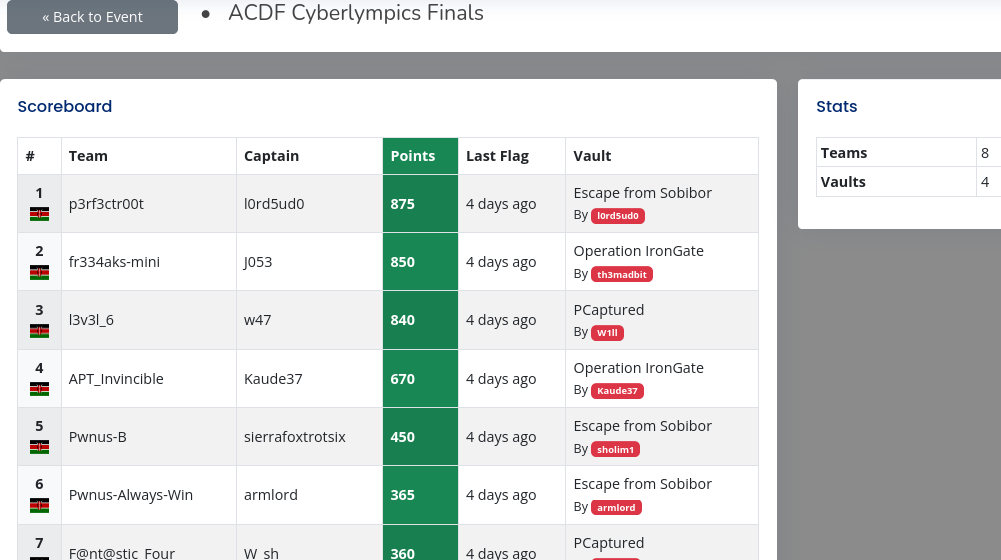
My team (Fr334aks-mini) secured 6th place for this qualifications round.

We secured position 2 at the finals held on 12 Jun 2025 10:30am - 12 Jun 2025 06:00pm

This writeup breaks down one of the challenges I solved in the qualifications round. Enough talk!

Reverse Engineering

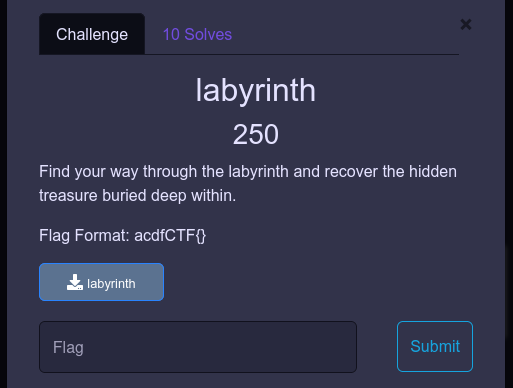
Labyrinth

We re given a file to find our way through…

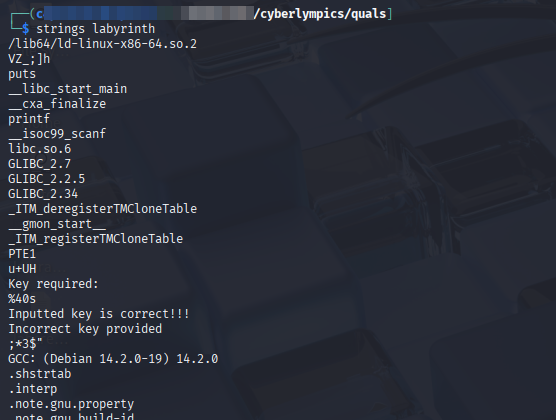
Checking the file type, we see it’s a stripped ELF, meaning the binary had its debugging symbols and other metadata removed.

Checking it’s strings shows nothing much.

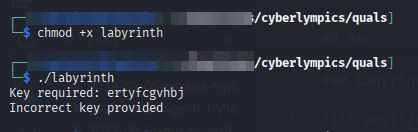
Let’s try and run it.

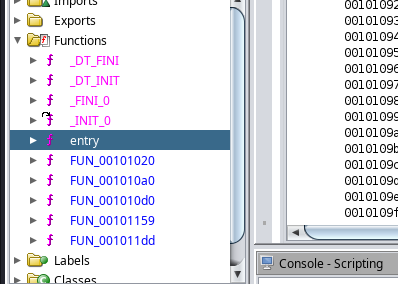
Seems we need some kind of a key! Let’s fire up ghidra and see what this litlle ELF has in store. We’ve got a couple functions.

We will want to check the main function or entry point of the binary.

• The prompt:

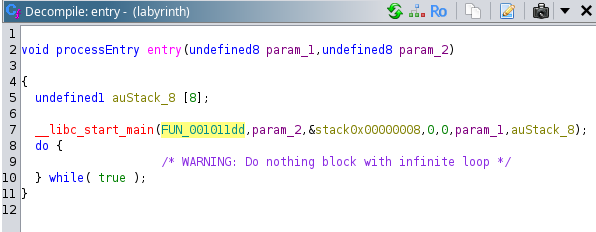
The entry point initializes function “FUN_001011dd”

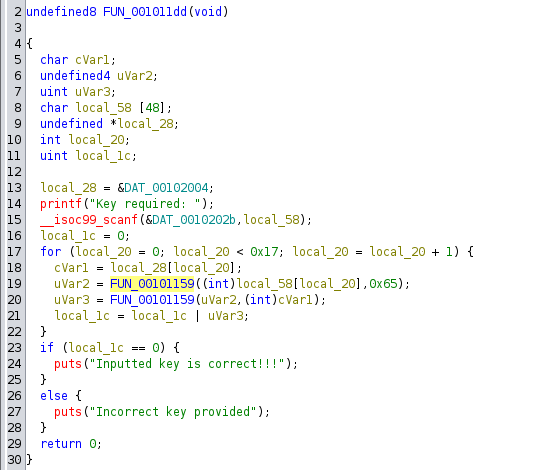
The program prompts for some key (“Key required: “). The “key” input is read into local_58 (which is a 48-byte buffer). It then compares each byte of the input (local_58) against a hardcoded array (local_28 = &DAT_00102004). If all comparisons pass (local_1c == 0), the key is correct. The function also calls in function “FUN_00101159”

• A custom bitwise comparison

This function compares two bytes (param_1 and param_2) bit-by-bit and returns a result: It iterates over each bit (from bit 31 down to bit 0). For each bit position:

• bVar1 = whether the bit is set in param_1.
• bVar2 = whether the bit is set in param_2.

The result for that bit is computed as: (!bVar2 || !bVar1) && (bVar1 || bVar2) which is equivalent to bVar1 != bVar2 (a XOR operation).

The final local_c is a 32-bit value where each bit is the XOR of the corresponding bits in param_1 and param_2.

• Key check condition

For each byte i (0 ≤ i < 0x17): If local_1c == 0, the key is correct. Since FUN_00101159 is just XOR, we can rewrite this as:

local_1c |= (input[i] ^ 0x65) ^ hardcoded_byte[i]

For local_1c to be 0, all XOR results must be 0: Just like in algebra:

(input[i] ^ 0x65) ^ hardcoded_byte[i] = 0

this simplifies to:

input[i] = hardcoded_byte[i] ^ 0x65

And this means we’d have to XOR the hardcorded bytes with 0x65 to get the key(should be our flag)

• Extracting the hardcoded bytes

The hardcoded array is at DAT_00102004 (referenced by local_28). We need to extract these bytes (length 0x17 = 23 bytes).

To extract these hardcoded bytes we need to dump the data section at 0x102004 We can use objdump, xxd, or even Ghidra. I used xxd for this one:

Since the hardcoded array is at DAT_00102004 (0x102004 in the binary), we can dump the binary and extract the bytes at this offset.

• First, let’s find the offset in the binary file:

The address 0x102004 is a virtual memory address (VMA) and we need to convert it to a file offset (where it physically resides in the binary).

• Let’s check the ELF sections:

We can see that the .rodata section (where hardcoded strings usually reside) is at:

Virtual Address (VMA): 0x2000
File Offset: 0x2000
Size: 0x62 (98 bytes)

The hardcoded key array is at 0x102004 (from the disassembly in ghidra). Since .rodata starts at 0x2000, this means:

0x102004 is inside .rodata (since 0x2000 ≤ 0x102004 ≤ 0x2000 + 0x62).

• Let’s calculate the file offset:

The binary is a PIE (Position-Independent Executable), so the actual .rodata VMA is 0x2000 (not 0x102000). Thus, the hardcoded array at 0x102004 is at:

File Offset = 0x2000 (start of .rodata) + (0x102004 - 0x102000) = 0x2004

(But remember 0x102004 - 0x102000 = 0x4 is the offset within .rodata.)

• Time to dump the bytes at 0x2004:

We need to dump 23 bytes (0x17 in hex) starting at 0x2004 in the file:

• Reconstructing the key

We need to XOR each byte with 0x65 to get the correct key. I used a short python code for this.

# Author: D_C4ptain

hardcoded_hex = "040601032631231e1d5517540b023a1254110d3a535018"
hardcoded_bytes = bytes.fromhex(hardcoded_hex)
key = bytes([b ^ 0x65 for b in hardcoded_bytes])
print(key.decode())

• Conclusion

The flag was the result of XOR-ing the hardcoded bytes (at DAT_00102004) with 0x65.

Till the next one.

And remember, there are many ways of killing Jerry!